Andréi Márcov
Andréi Andréyevich Márkov (Андре́й Андре́евич Ма́рков) ( 14 de junio de 1856-20 julio de 1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades.
Márkov nació en Riazan. Rusia. Antes de los 10 años su padre, un funcionario estatal, fue trasladado a
San Petersburgo donde Andréi entró a estudiar en un instituto de la ciudad. Desde el principio mostró cierto talento para las matemáticas y cuando se graduó en 1874 ya conocía a varios matemáticos de la Universidad de San Petersburgo donde ingresó tras su graduación.
Su trabajo teórico en el campo de los procesos en los que están involucrados componentes aleatorios (procesos estocásticos) darían fruto en un instrumento matemático que actualmente se conoce como cadenas de Márkov : secuencias de valores de una variable aleatoria en las que el valor de la variable en el futuro depende del valor de la variable en el presente, pero es independiente de la historia de dicha variable. Cadenas de Márkov hoy día, se consideran una herramienta esencial en disciplinas como la economía, la ingeniería, la investigación de operaciones y muchas otras.
CADENAS DE MÁRCOV
En la teoría de la probabilidad, se conoce como cadena de Márkov a un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un evento depende del evento inmediatamente anterior. En efecto, las cadenas de este tipo tienen memoria. "Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Márkov de las series de eventos independientes, como tirar una moneda al aire o un dado.
Matriz de transición
Si pij es la probabilidad de transición del estado i al estado j , ( 0<= i, j <=M)
Se denomina matriz de transición o matriz de probabilidades de transición de un paso
Propiedad:
Las filas de la matriz de transición suman 1.
S
Es una matriz cuadrada
Los números que componen la matriz van de 0 a 1, ya que son probabilidades.
Ejemplo:
SOLUCIÓN:
Los estados de la cadena los denotaremos por { 0, 1 , 2} haciendo
corresponder el 0 al bajo y 1 y 2 al primer y segundo piso respectivamente.
Las probabilidades de transición son:
p00 = P(Rn=0 / Rn-1=0), esto es la probabilidad de que el ascensor se encuentre en
la planta baja si en la etapa anterior estaba en la planta baja. Obviamente es 0,
porque se supone que de etapa a etapa el ascensor se mueve.
p01 = P(Rn=1 / Rn-1=0), esto es la probabilidad de que el ascensor se encuentre en
la planta primera si en la etapa anterior estaba en la planta baja. Obviamente es
½. Basta leer el enunciado.
Y así sucesivamente vamos obteniendo las distintas probabilidades de transición
cuya matriz es:
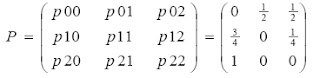 Probabilidad de transicion en K pasos. Teorema Chapman- Kolmogorov
puesto que las probabilidades de transicion son estables en el tiempo, podemos interezarnos en conocer las probabilidades de transicion despues de k pasos, definidas formalmente como:
Esto es la probabilidad de que el proceso se encuentre en el estado j si k estapas antes se encontraba el estado i.
Si conocemos pij, podemos calcular las pij^(k) haciendo el siguiente razonamiento :si al cabo de m< k pasos nos encontramos en el estado e, la probabilidad de alcanzar el estado j despues de k-e pasos sera:
Como el estado intermedio e puede ser cualquiera, podemos determinar una expresion para la probabilidad de transicion de k pasos:
Probabilidad de transicion en K pasos. Teorema Chapman- Kolmogorov
puesto que las probabilidades de transicion son estables en el tiempo, podemos interezarnos en conocer las probabilidades de transicion despues de k pasos, definidas formalmente como:
Esto es la probabilidad de que el proceso se encuentre en el estado j si k estapas antes se encontraba el estado i.
Si conocemos pij, podemos calcular las pij^(k) haciendo el siguiente razonamiento :si al cabo de m< k pasos nos encontramos en el estado e, la probabilidad de alcanzar el estado j despues de k-e pasos sera:
Como el estado intermedio e puede ser cualquiera, podemos determinar una expresion para la probabilidad de transicion de k pasos:
Haciendo m = 1, m=k-1 obtenemos las ecuaciones de Chapman - Kolmogorov, que permiten obtener las expresiones de las propiedades de transicion en el estado k a partir de las k-1
Lo que indica las ecuaciones es que pueden obtenerse matrices P^(k) de transicion de k pasos a partir de las potencias de la matriz P.
Es decir, que las sucesivas potencias de la matriz P indican las probabilidades de transicion en tantas transicones como se indica en el indice. Esto puede generalizarse aun mas observando que la P^(1) representa la probabilidad de una transicion y que P^(0) = I es la probabilidad en cero transiciones: si no ha habido transicion, el estado es el mismo y por lo tanto la matriz que representa la no.transicion es la matriz identidad.
EJEMPLO
La siguiente matriz de transición muestra las probabilidades de transición de un estado actual, a un estado posterior
Dicha matriz muestra el comportamiento de transición de los clientes de telefonía movil, de las comañias Tigo, Comcel y Movistar.
Con base a la matriz de probabilidad actuales, calcular la matriz de probabilidad de los estados
P1,P2,P3,P4 Y P5
Cadenas Absorbentes- Matriz Absorbente.
Una cadena de Markov con espacio de estados finito se dice absorbente si se cumplen las dos condiciones siguientes:
1. La cadena tiene al menos un estado absorbente.
2. De cualquier estado no absorbente se accede a algún estado absorbente.
Si denotamos como A al conjunto de todos los estados absorbentes y a su complemento como D, tenemos los siguientes resultados:
Su matriz de transición siempre se puede llevar a una de la forma

donde la submatriz Q corresponde a los estados del conjunto D, I es la matriz identidad, 0 es la matriz nula y R alguna submatriz.
 , esto es, no importa en donde se encuentre la cadena, eventualmente terminará en un estado absorbente.
, esto es, no importa en donde se encuentre la cadena, eventualmente terminará en un estado absorbente.
Ejemplo resuelto:
Ingecosmos vende partes decamiones, cuando una empresa compra a ingecosmos, le dan tres meses para pagar si la cuenta no se salda en ese periodo, ingecosmoscancela la cuenta y la remite a una cuenta de cobranza, y da por terminada, por tanto ingecosmo clasifica las cuentas nuevas, con un mes de retraso, con dos meses de retraso, tres meses de retraso, pagadas o incobrables, ingecosmos estudio sus antiguos registros y descubrio que.
a) El 70% de las cuentas nuevas se pagan en un mes, el 60% de las cuentas con un mes de retraso se pagan al final de mes.
b) el 50% de las cuentas con dos meses de retraso se pagan al final del ultimo mes
c) el 60% de las cuentas con tres meses de retraso se remiten a una cuenta de cobranzas
1) Forme la matriz de transición
2) Cual es la probabilidad de que una nueva cuenta se liquide
3) Cual es la probabilidad de que una cuenta de un mes de retraso se vuelva incobrable
4) Si las ventas de ingecosmos son en promedio $ 125 000 al mes, cuanto dinero se aasentara como deuda incobrable
1) Matriz de transición, los estados son, cuentas nuevas , con 1 me, 2 meses y 3 meses de retraso, cuentas pagadas e incobrables.
2) Para calcular la probabilidad que una nueva cuenta se liquide, debemos seguir los siguentes pasos
1 Encontrar la matriz fundamental X
La matriz I
La matriz (I-N)
Ahora la matriz fundamental es
2do paso es multiplicar la matriz fundamental por la matriz A absorbente
Rta// la probabilidad que una nueva cuenta se liquide es de 0,964
3) la probabilidad de que una cuenta de un mes de retraso se vuelva incobrable, también es posible identificarla en la ultima tabla de potabilidades y es de 0,12
4) Debido a que la probabilidad de que una cuenta nueva se vuelva incobrable es de 0,036 . Entonces si multiplicamos $ 125 000 * 0,036 = $ 4 500, tenemos la cantidad que se asentara como incobrable mensualmente , para calcular la cantidad al año multiplicamos $ 4500 * 12 = $ 54 000 y aquí tenemos la cantidad que se asentara como incobrable en el año.
Matriz Ergodica
Una cadena de Markov es ergodica si todos sus estados son no nulos, no periodicos y
recurrentes.
Propiedad: Las cadenas de Markov ergodicas cumplen la siguiente propiedad: El limite
ij
Las probabilidades lımites πj se denominan probabilidades de estado estable.
Propiedad: Si los lımites anteriores existen, entonces
Cadenas recurrentes
Una cadena de Markov se dice positivo-recurrente si todos sus estados son positivo-recurrentes. Si la cadena es además irreducible es posible demostrar que existe un único vector de probabilidad invariante y está dado por:

Cadenas regulares
Una cadena de Markov se dice regular (también primitiva o ergódica) si existe alguna potencia positiva de la matriz de transición cuyas entradas sean todas estrictamente mayores que cero.
Cuando el espacio de estados E es finito, si P denota la matriz de transición de la cadena se tiene que:
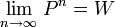
donde W es una matriz con todos sus renglones iguales a un mismo vector de probabilidad w, que resulta ser el vector de probabilidad invariante de la cadena. En el caso de cadenas regulares, éste vector invariante es único.
Estado estable
Las probabilidades de estado estable πj satisfacen las ecuaciones de estado estable
Son, en total, M+2 ecuaciones con M+1 incognitas. Una de las primeras M+1 ecuaciones
depende de las otras.
Propiedad: Las probabilidades de estado estable se relacionan con los tiempos medios de retorno
de la siguiente manera:
existe y es independiente del estado inicial i. Lo denominaremos πj :






























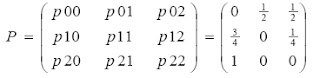








 , esto es, no importa en donde se encuentre la cadena, eventualmente terminará en un estado absorbente.
, esto es, no importa en donde se encuentre la cadena, eventualmente terminará en un estado absorbente.